 2022 Project RUBI (Rebel Upward Bound Institute)
2022 Project RUBI (Rebel Upward Bound Institute)

Math major Joseph Bishop has been awarded a Waldemar J. Trjitzinsky Scholarship by the American Mathematical Society for the 2021-2022 academic year.

Learn about what it's like to major in Mathematics at the University of Mississippi.

Math faculty Sandra Spiroff and Kelvin Holmes traveled with students Trinity Roebuck, Bria Taylor, and Tia Garland to the 2020 Gulf States Math Alliance Conference in Baton Rouge, LA at Southern University and A&M College.

Professor Arthur Benjamin, from Harvey Mudd College, explains to students and faculty members the mathematics behind several card tricks.
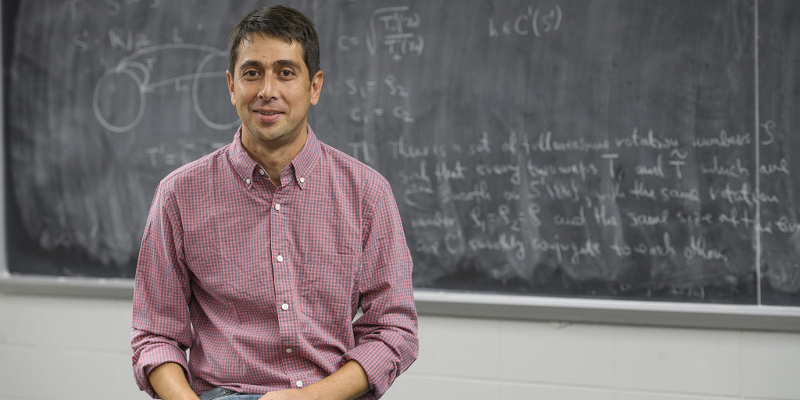
Saša Kocić, assistant professor of mathematics, has been chosen for funding under NSF’s Established Program to Stimulate Competitive Research, a program designed to help junior investigators in EPSCoR-eligible states develop career-spanning collaborations through extended visits to other premiere research institutions around the nation.

Graduate students discuss homework as well as assist undergraduates with Calculus in the tutoring room.